【读书笔记】数据结构与算法分析 - C 语言描述 - 第一部分 - 基础知识
3 min read
第一章 引言
- 连通性问题:
- 两个操作:查找(find)、并集(union)
- 快速-查找(quick-find):N 个对象,M 次合并:MN
- 快速-合并(quick-union):N 个对象,M 对:MN/2
- 加权快速-合并(weighted quick-union):遍历 2lgN 个指针:线性
- 带等分路径压缩的加权快速-合并:保证线性
- 在线算法(online):能处理的数据没有限制
第二章 算法分析的原理
- 算法分析的种类:
- 最坏情况(Worst Case):任意输入规模的最大运行时间(Usually)
- 在任何输入下运行时间的一个上界
- 平均情况(Average Case):任意输入规模的期待运行时间(Sometimes)
- 最佳情况(Best Case):通常最佳情况不会出现(Bogus)
- 最坏情况(Worst Case):任意输入规模的最大运行时间(Usually)
- 基本思路:
- 忽略掉那些依赖于机器的常量
- 关注运行时间的增长趋势
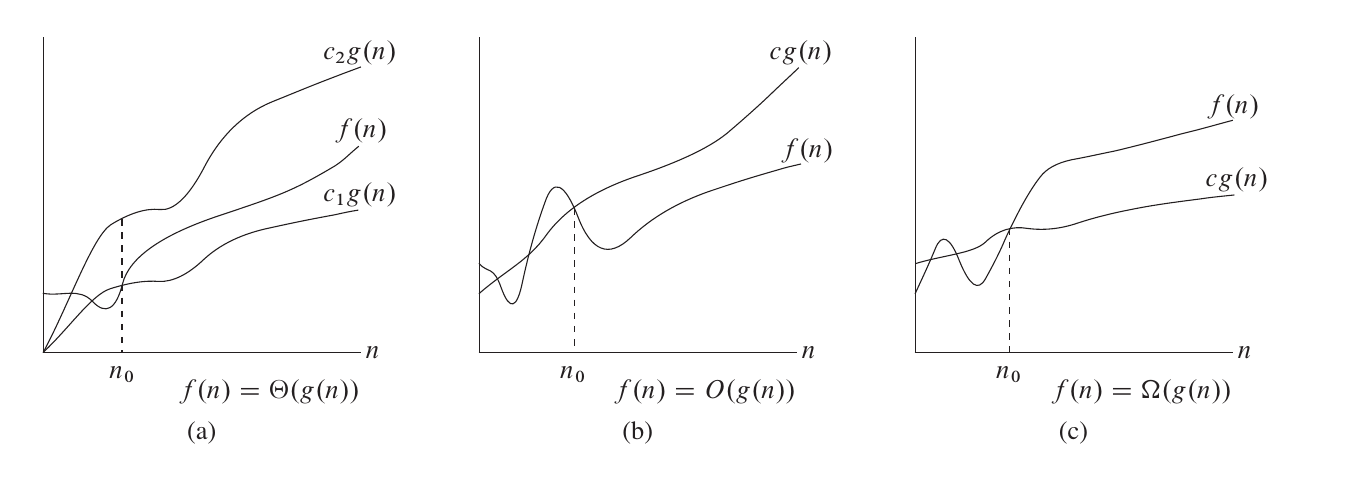
- 渐近记号:
- 尽管技术上 theta 符号较为准确,但通常仍然使用大 O 符号表示
- 大 O 符号:只有渐近上界
- 表示最坏运行情况的上界
- T(n) = O(n^3) 等同于 T(n) ∈ O(n^3):T(n) 的渐近增长不快于 n^3
- theta(西塔)符号:渐近地给出了一个函数的上界和下界
- T(n) = Θ(n^3) 等同于 T(n) ∈ Θ(n^3):T(n) 的渐近增长与 n^3 一样快
- omega(欧米伽)符号:只有渐近下界
- 采用记号 lgN = log_2N:改变一个对数的底只是把对数的值改变了一个常数倍,所以当不在意这些常数因子时可使用这个简便的记法
- 常见复杂度:
- 常量:O(1)
- 对数:O(lgN)
- 线性:O(N)
- 线性对数:O(NlgN)
- 平方:O(N^2)
- 立方:O(N^3)
- 指数:O(2^N) O(k^N)
- 阶乘:O(N!):旅行商问题
- floor(x):向下取整 x。设 x = 4.5,floor(x) = 4
- ceil(x):向上取整 x。设 x = 4.5,ceil(x) = 5
- 调和级数:H_N = 1 + 1/2 + 1/3 + … + 1/N